
Централните проекции на Платоновите тела оформят красиви фигури, които показват структурата и симетриите на тези обекти.

Нека всички върхове на правилен многостен се допират в сфера в тримерното пространството. Поставяме сферата върху равнина, точката на докосване остава фиксирана, “Южният полюс” се проектира в допирателната точка, а “Северният полюс” обратно - проектира се в безкрайността.
Всяка друга точка на повърхността на сферата се проектира на уникално място върху равнината, в точка, получена от пресичането на равнината с линия, определена от точката на Северния полюс и точката от сферата, която искаме да изобразим.
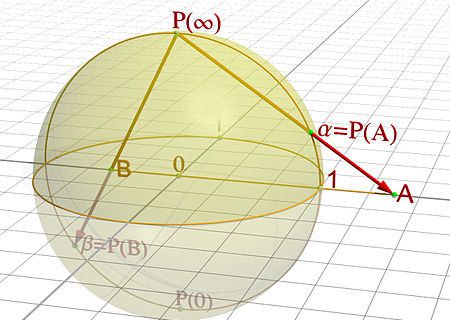
Ако два върха са свързани с ребро в многостена, след това образът на ръба ще е отсечка в равнината, свързваща образите на два върха.
Изображението на ръбовете на многостена се нарича диаграма на Шлегел, на името на Виктор Шлегел, който е измислил този вид схема през 1883 г.
Диаграмите на Виктор Шлегел
Станислав Фердинанд Виктор Шлегел (Victor Schlegel) е немски математик от края на 19-ти, началото на 20-ти век. Той разработва двумерно представяне на структурата на на тримерни многостени като всеки връх от тялото се проектира в диаграмата на Шлегел като точка, всеки ръб като линия. Страничните повърхности на тялото, ограничени от ръбовете се проектират като многоъгълници. Диаграмата не се самопресича.
Смисълът е да може да се покаже в (n-1) размерно пространство структурата (връхове, ръбове, страни и т.н.) на n -размерни тела. Проекцията и самият многостен са топологически еквивалентни.
В диаграмите на Шлегел не се обръща внимание на дължините на изходния многостен, се запазва общата архитектура: броя на ребрата събиращи се един и същи връх, броя на стените, които се съединяват в едно и също ребро, броя на страните на стените и броя на самите стени.
Всеки многостен може да има различни изображения, образувани от централно проектиране от северния полюс, в зависимост от това как многостенът се завърта в сферата. Ще разгледаме само такива диаграми на Шегел със специална характеристика, а именно, центърът на стената, която е най-близо до северния полюс и образът ѝ съдържа образите на всички останали върхове.
Построяване

Диаграмите на Шлегел може да се построят по два начина:
- Изглед в перспектива с фокус външна точка на многостена, над центъра на една стена. Всички върхове и всички краища на тялото се проектират върху равнина на тази стена.
- Еквивалентно е на отстраняване на стената върху проекционната равнина и "разширяване" на отвора докато останалата част от повърхността на изпъкналия многостен не се изравни върху равнината. Този метод дава всеки път отличен резултат.
Платоновите тела в диаграми на Шлегел
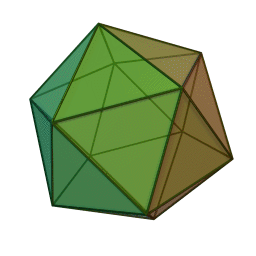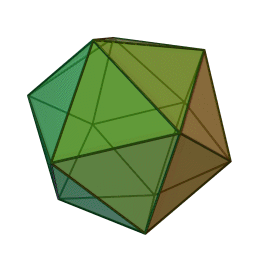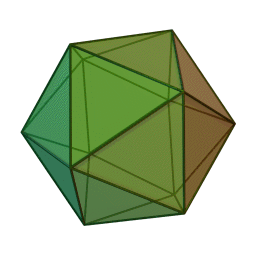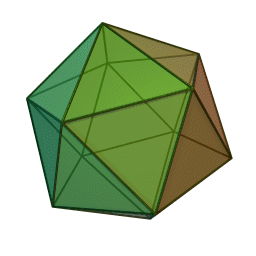
Шлегелoвите диаграми на многостени може да се разглеждат приблизително като сянката на скелета им върху плоска повърхност.
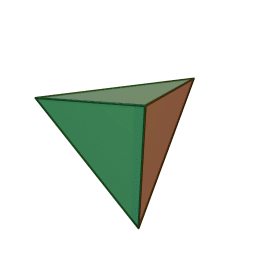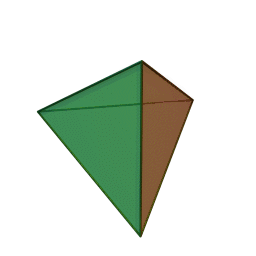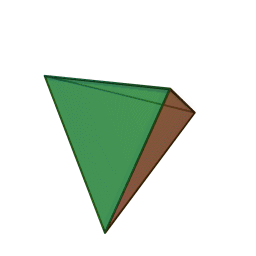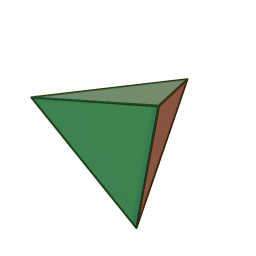
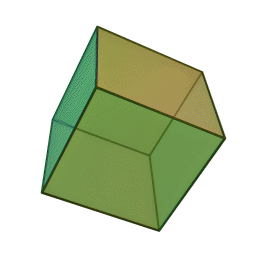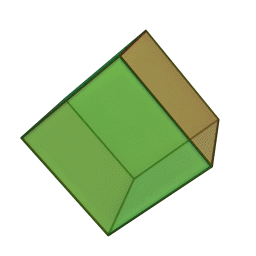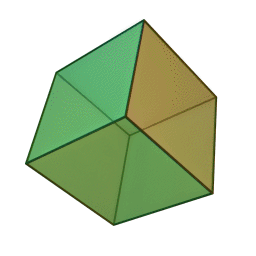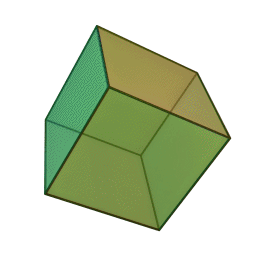
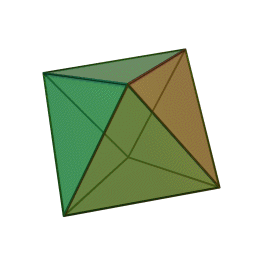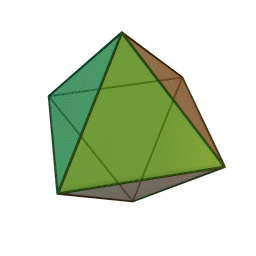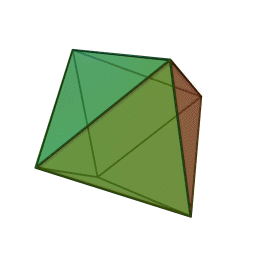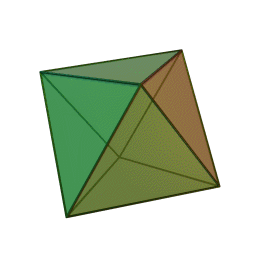
| Тетраедър | Куб | Октаедър | Додекаедър | Икосаедър |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
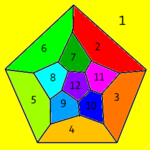
Жълтата външна зона представя отстранената стена при построяването на стереографската проекция и не трябва да се пропуска. Тази жълта област показва същия брой върхове и ръбове като отстранената стена.
Как изглеждат Платоновите тела в диаграми на Шлегел
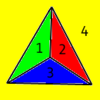
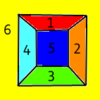
Шлегеловата диаграма на куба е познатото "квадрат рамките на квадрат". За тетраедъра, диаграмата на Шлегел е триъгълник с върхове, свързани с неговата средна точка.
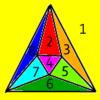
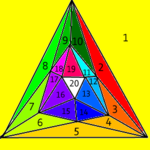
За да се позиционира октаедъра за Шлегелова диаграма, трябва да се завърти многостенът така, че две от триъгълните му стени да са хоризонтални. В резултат от проекцията, образът на горната повърхност ще е голям равностранен триъгълник, а образът на долната повърхност е по-малък равностранен триъгълник завъртян на половин оборот. Образите в равнината на другите шест триъгълника на октаедъра са триъгълници, на които всеки връх се присъединява с върховете на вътрешния триъгълник с върховете на външния.

В съответната схема за икосаедъра, 12-те върха са подредени в три вложени полигони: големият равностранен триъгълник съдържа правилен шестоъгълник, който от своя страна се състои от малки равностранни триъгълници.
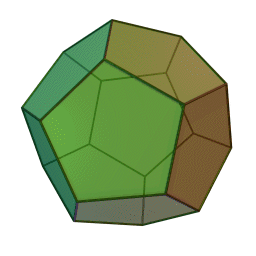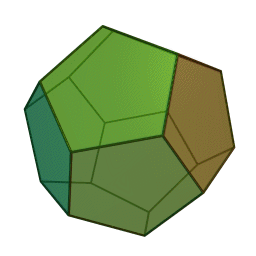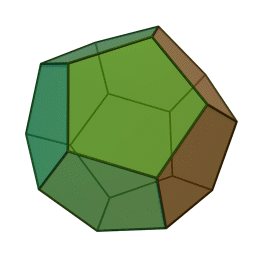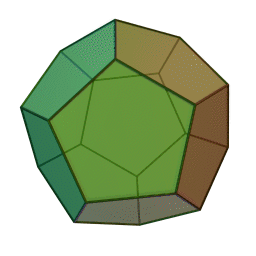
Шлегеловата схема на додекаедъра има 20 върха по подобен начин, подредени в три вложени полигони: голям правилен петоъгълник, който съдържа 10 неравностранни петоъгълника, обграждащи малък правилен петоъгълник.
Диаграмите на Шлегел се използват широко и днес за представяне на строежа на сложни молекули, фулерени и други.
Диаграмите на Шлегел за визуализиране на четиримерни тела
В началото на 20 -ти век, диаграмите на Шлегел се оказаха изненадващо полезни инструменти за изучаване на топологичните и комбинаторни качества на политопите.
В 3 измерения, диаграмата Шлегел се състои от проектиране на многостен във вид на плоска равнинна фигура, разделена на области, представящи стените на изходния многостен. В 4 измерения, тя ще се състои от проекцията на 4-мерни тела в един многостен разделен на вътрешни отделения, представящи клетките на оригиналния политоп. Обикновено диаграмите на Шегел се използват за да се визуализират четиримерни тела като триизмерни обекти.
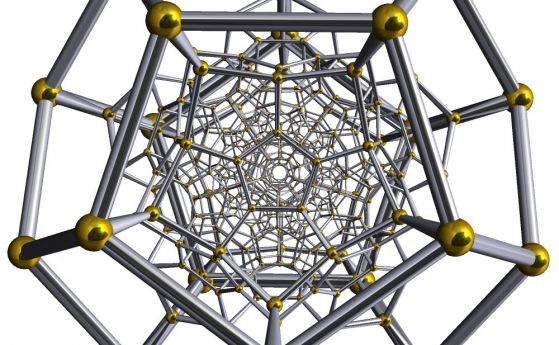
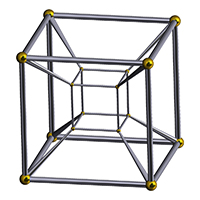
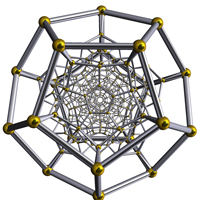
Можем да създадем Шлегелови диаграми на правилните четиримерни политопи посредством централно проектиране от четиримерното пространство към тримерното пространство, аналог на централното проектиране от тримерното пространство върху равнина. Шлегеловият многостен на хиперкуба е куб в рамките на куб като са свързани съответните върхове.
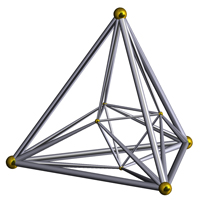
Както Шлегеловата диаграма на тетраедър е триъгълник с върхове свързани към централната точка, така диаграмата на Шлегел на четиримерния многостен-симплекс е тетраедър с върхове, свързани към една централна точка. Шестте триъгълници се присъединяват към тази централна точка и към краищата на големия тетраедър като разделят вътрешността на тетраедъра на четири триъгълни пирамиди.
Едно единствено изображение по Шлегел на многостен може да изглежда доста объркващо. Още през миналия век, математиците са експериментирали с стереоскопични двойки на геометричните обекти.
Стереодвойката на тесеракта се изобразява като две проекции на триизмерното пространство. Това е опит да се покаже дълбочината като четвърто измерение. Стереодвойката се гледа така, че всяко око да вижда само една от тези снимки и тогава ще се появяви стереоскопична картина.

Въпреки че тази техника все още е полезна при изучаване на сложни конфигурации, най-ефективният начин да се видят обектите в тримерното пространство е да "се разходим" в тях и да наблюдаваме телата в движение в анимации.
Източници:
Dimensions, Jos Leys - Étienne Ghys - Aurélien Alvarez
Schlegel Diagrams of Polyhedra, Thomas F. Banchoff
Schlegel Polyhedra for Regular Polytopes, Thomas F. Banchoff






























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон