
Задачата за вписаните правоъгълници задава един привидно прост въпрос: може ли в затворен контур да се намерят винаги четири точки, които да определят върховете на правоъгълник с предварително определено съотношение на страните?
В средата на март двама математици Джошуа Грийн (Joshua Greene) и Андрю Лоб (Andrew Lobb) се оказват в карантина и в опит да се приспособят, докато наоколо се разраства пандемията COVID-19, те решават да се справят с тази наглед проста, но нерешена за 100 години задача в геометрията.
И на 19 май, когато части от света тепърва започват да се отварят, те се появяват по свой начин и публикуват решението.
Въпреки че този „проблем на вписаните правоъгълници“ изглежда като задача, която един гимназист може да реши с линийка и пергел, той остава нерешен въпреки усилията на най-добрите математици в продължение на десетилетия. И когато Грийн и Лоб се заемат с нея, изобщо не са уверени, че ще се справят.
От всички различни проекти, над които работи, Грийн смята: „Мислех, че това е най-малко обещаващият“.
Преосмисляне на правоъгълниците
През 1911 г. немският математик Ото Топлиц (Otto Toeplitz) предполага, че всяка затворена крива (т.е. която започва и завършва на едно и също място) съдържа четири точки, които свързани, образуват квадрат. Докато предположението за вписаните квадрати бързо е доказано за непрекъсната (без разкъсвания) и гладка (без ъгли) затворена крива през 1929 г., задачата все още не е решена за непрекъснати негладки криви.
Проблемът, който Грийн и Лоб решават, също включва криви, които са гладки и следователно непрекъснати. И вместо да определят дали тези криви винаги имат четири точки, които правят квадрат, те изследват дали тези криви винаги имат набори от четири точки, които образуват правоъгълници с всякакво съотношение на страните, което означава съотношенията на дължините на две съседни страни. За квадрат пропорцията е 1:1, докато за много телевизори е 16:9.
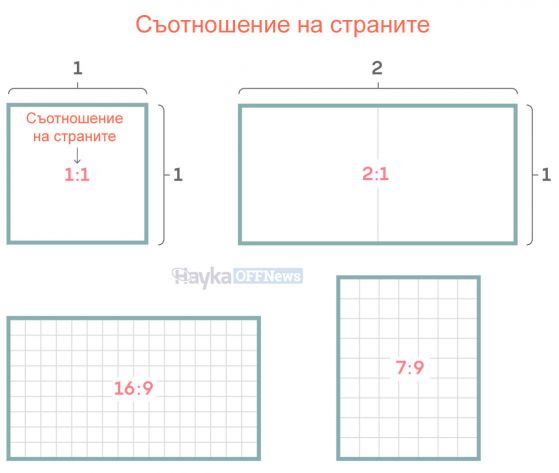
Илюстрация, показваща различни съотношения на страните на правоъгълник. Кредит: Samuel Velasco/Quanta Magazine.
Първият фундаментален напредък по проблема с вписаните правоъгълници е постигнат в доказателство от края на 70-те години на Хърбърт Вон (Herbert Vaughan). Доказателството инициира нов начин на мислене в геометрията на правоъгълника и установи методи, които много математици, включително Грийн и Лоб, впоследствие избират.
Вместо да се гледа на правоъгълника като за четири свързани точки, Вон го разглежда като две двойки точки, които имат определена връзка помежду си.
 Схема, показваща, че диагоналите на правоъгълника са еднакви по дължина и споделят средна точка. Кредит: Samuel Velasco/Quanta Magazine.
Схема, показваща, че диагоналите на правоъгълника са еднакви по дължина и споделят средна точка. Кредит: Samuel Velasco/Quanta Magazine.
Представете правоъгълник, чиито върхове са ABCD по посока на часовниковата стрелка отгоре-наляво. В този правоъгълник разстоянието между точките AC (диагонал на правоъгълника) е същото като разстоянието между точките BD (другия диагонал). Двете отсечки се пресичат в средната им точка.
Затова, ако търсите правоъгълници на затворен контур, един от начините да ги намерите е да потърсите двойки точки върху него, които споделят това свойство: Те образуват отсечки с еднаква дължина със една и съща средна точка. И за да се намерят, е важно да се измисли систематичен подход към тях.
За да добием представа какво означава това, нека започнем с нещо по-просто. Да вземем стандартната числова линия. Нека изберем две точки върху нея - да кажем числата 7 и 8 - и да ги отбележим като една точка в равнината xy (7, 8). Допустими се и двойки от една и съща точка (7, 7). Сега да разгледаме всички възможни двойки числа, които могат да бъдат извлечени от числовата ос. Ако начертаем всички тези двойки точки, бихме могли да запълним цялата двумерна xy-равнина. Друг начин за това е да се каже, че равнината xy „параметризира“ или събира по подреден начин всички двойки точки на числовата линия.
Вон прави нещо подобно за двойки точки на затворена крива. (Подобно на числовата линия, тя е едномерна, само че е крива и затворена). Той разбира, че ако се вземат двойки точки от кривата и ги начертаете - без значение коя точка е координатата x и коя е y - не се получава плоска xy-равнина. Вместо това се получава изненадваща форма: лентата на Мьобиус, която е двумерна повърхност, която има само една страна.
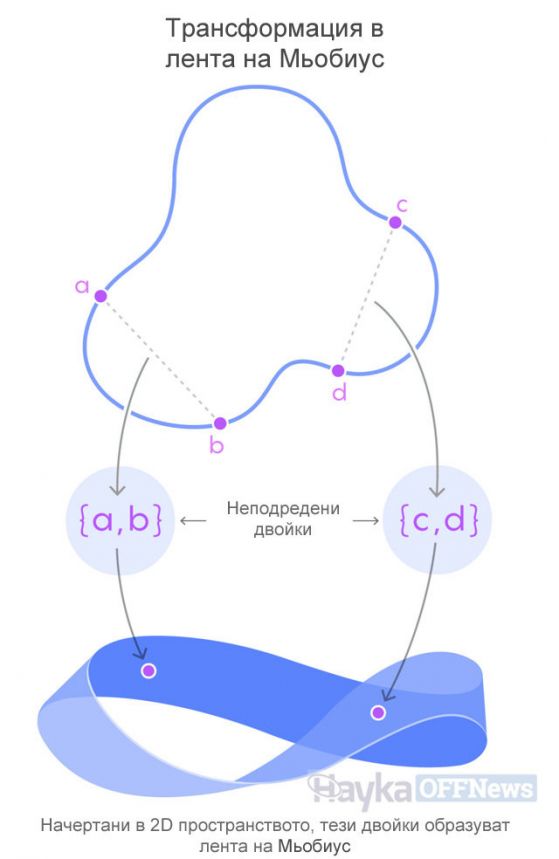
Схема, показваща идеята за начертаването на двойки точки на затворената крива като лента на Мьобиус. Кредит: Samuel Velasco/Quanta Magazine.
По някакъв начин това има смисъл. За да стане ясно защо, да изберем двойка точки на кривата и да ги обозначим с x и y. Сега да изминем пътя от x до y по едната дъга на кривата, докато преминем по контура от y до x по допълващата дъга на кривата. Докато правим това, ние обхождаме всички двойки точки на кривата, започвайки и завършвайки с неподредената двойка (x,y) - тоест двойка числа, при които е без значение кое е x и кое - y. Но докато преминаваме и се връщаме там, където сме започнали, само че с преобърната ориентация. Такава преобърната ориентация на затворената крива от неподредени точки образува лентата на Мьобиус.
Тази лента на Мьобиус предоставя на математиците нов обект, който да анализират, за да решат задачата за вписаните правоъгълници. И Вон използва този факт, за да докаже, че всяка такава крива съдържа поне четири точки, които образуват правоъгълник.
Четириизмерни отговори
Доказателството на Грийн и Лоб е изградено върху работата на Вон. Но също така комбинира няколко допълнителни резултати, достъпни от съвсем наскоро.
Един от първите важни инструменти на тяхното доказателство се появява през ноември 2019 г., когато аспирант от Принстън на име Коул Хугелмайер (Cole Hugelmeyer) публикува документ, който представя нов начин за анализ на лентата на Мьобиус на Вон. Тази работа включва математически процес, наречен вграждане (embedding), при който се взема обект и се "трансплантира" в геометричното пространство. В крайна сметка Грийн и Лоб възприемат техниката на Хугелмайер и я прилагат в още едно геометрично пространство.
Ето един прост пример за това какво е вграждане (ембединг).
Започваме с едномерна линия. Всяка точка от тази еднодименсиална линия се определя от едно число. Сега да „вградим“ тази линия в двуизмерно пространство - което ще рече, просто да я начертаем в равнината.
След като вградите линията в xy-равнината, всяка точка от нея се определя от две числа - x и y координатите, които определят точно къде в равнината се намира тази точка. Като се има предвид този подход, след това можем да започнем да анализираме линията, използвайки техниките на двумерната геометрия.
Идеята на Хугелмайер е да направи нещо подобно за лентата на Мьобиус, но вместо това да се вгради в четиримерно пространство, където може да се използва функции на четириизмерната геометрия, за да докажат резултатите, които са нужни за правоъгълниците.
„По същество имаме нашата лента на Мьобиус и за всяка точка от нея й даваме четири координати. Даваме на всяка точка своеобразен адрес в четиримерно пространство“, обяснява Лоб.
Хугелмайер създава тези адреси по начин, който се оказва особено полезен за общата цел да се намерят правоъгълниците на кривата. Може да разглеждате тези адреси, подобно на пощенските адреси, като се присвоява на всяка точка от кривата държава, град, име на улица и номер.
За да направи това, той започва с дадена точка на лентата на Мьобиус и проследява двете точки на оригиналната затворена крива, която представя. След това намира средната точка на тази двойка точки и определя нейните x и y координати. Това са първите две стойности в четириизмерния адрес (като държавата и града).
След това той измерва разстоянието по права линия между двете първоначални точки на кривата. Тази дължина става третата стойност в четириизмерния адрес (като име на улицата). И накрая, той изчислява ъгъла, образуван там, където линията през двете първоначални точки пресича оста x. Този ъгъл става четвъртата стойност в четириизмерния адрес (като номер на улицата). Тези четири стойности ефективно ни казват всичко за двойката точки на кривата.

Схема, обясняваща как на всяка двойка точки от затворена крива може да бъде присвоен уникален четириизмерен адрес. Кредит: Samuel Velasco/Quanta Magazine.
Упражнението може да изглежда сложно, но се изплаща бързо на Хугелмайер. Той завърта вградената лента на Мьобиус да речем малко вляво. Завъртяната лента на Мьобиус се измества от оригинала, така че двете копия се пресичат взаимно. (Тъй като въртенето се извършва в четиримерното пространство, точният начин, по който двете копия на лентата на Мьобиус се припокриват, е трудно да се визуализира, но е лесно математически.)
Това пресичане е много важно. Точката на пресичане между завъртяната лента на Мьобиус и незавъртяната лента на Мьобиус съответства точно на две двойки точки на първоначалната затворена крива, които образуват върховете на правоъгълник.
Защо?
Първо, да не забравяме, че правоъгълникът може да се представи като две двойки точки, които споделят средна точка и са на еднакво разстояние една от друга. Това е точно информацията, кодирана в първите три стойности на четириизмерния адрес, присвоен на всяка точка от вградената лента на Мьобиус.
Второ, възможно е да завъртите лентата на Мьобиус в четиримерно пространство, така че да променяте само една от координатите в четирикоординатния адрес на всяка точка - като промяна на уличните номера на всички къщи едновременно, но оставяйки името на улицата, град и държава непроменени.
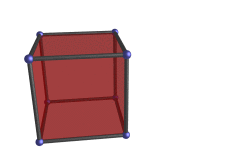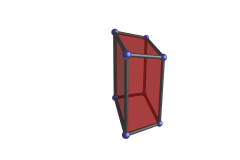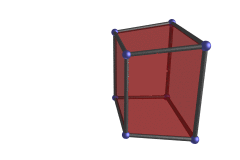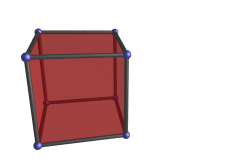
За по-геометрична пример, представете си как се държи куб, ако се променят само неговите х координати, а не У и Z координати. Ще използваме триизмерна аналогия, за да изследваме проекцията на 3D куб, докато се върти около 4D ос. Това много ще ни помогне да разберем проекциите на 4D-обектите.
 |
 |
|
Да разгледаме 2D квадрат, който се върти в 3D. Забележете, че изображението на плочката се появява като квадрат, само когато се гледа анфас. Когато се вижда под ъгъл, изглежда не като квадрат, а като трапец. Неговите вътрешни ъгли се променят и външният ръб изглежда като че ли се удължава и свива, тъй като се върти около 3D ос. Въпреки това, ние си знаем, че квадратът не променя своите вътрешни ъгли или дължината на страните си, той просто изглежда по този начин, защото се вижда в перспектива. |
Кубът все едно се обръща наопаки и налице като чорап. Една от стените му като че ли пораства и се свива, а неговите странични стени се разкривяват в трапеци. Кубът обаче всъщност си остава куб, но изглежда така, защото се върти през 4-тото измерение. По-точно се върти в равнината XW (равнината, определена от координатни оси Х и W). |
|
За да разберем този странен ефект, помислете как би изглеждала на едно 2D същество в анимацията вляво на квадрат, който се върти около 3D ос. Единствените ротации, които то знае, са ротации в равнината и никоя от тях не обръща нещата така. Тъй като няма никакъв опит в 3D ротациите, ще възприеме, че квадратът се смачква и се обръща наопаки и обратно по невъзможен начин. Но в действителност, квадратът не се обръща наопаки, той просто прави едно съвсем нормално въртене през 3D. |
|
Хюгелмайер обяснява как да се завърти лентата на Мебиус в четиримерното пространство, така че двете координати, кодиращи средната точка между двойки точки, да останат същите, както и координатата, кодираща разстоянието между двойките точки. Завъртането променя само последната координата - тази, кодираща информация за ъгъла на линейния сегмент между двойките точки.
В резултат на това пресечната точка между завъртяното копие на лентата на Мьобиус и оригинала съответства точно на две отделни двойки точки на затворената крива, които имат една и съща средна точка и са на едно и също разстояние. Което означава, че пресечната точка съответства точно на четирите върха на правоъгълник на кривата.

Проста диаграма, показваща как завъртяната крива може да създаде точка на пресичане със старата крива. Кредит: Samuel Velasco/Quanta Magazine.
Тази стратегия за използване на пресечна точка между две пространства, за да се намерят точките, които търсим, отдавна се използва в работата по проблемите с вписването на квадратите и правоъгълниците.
Хугелмайер използва стратегията на пресичане в четиримерно пространство и извича повече от всеки друг преди него. Лентата на Мьобиус може да се завърти под всякакъв ъгъл между 0 и 360 градуса и той доказва, че една трета от тези завъртания дават пресечна точка между оригинала и завъртяното копие. Този факт се оказва равностоен на това, че в затворена крива може да се намерят правоъгълници с една трета от всички възможни съотношения на страните.
Резултатът на Хугелмайер е и провокативен: Ако четиримерното пространство е толкова полезен начин за щурмуване на проблема, защо бе полезно само за една трета от всички правоъгълници?
"Трябва да може да получим и другите две трети", коментира Грийн. "Но как?"
Симплектично пространство
Още преди да бъдат затворени от пандемията, Грийн и Лоб се интересуватот проблема с вписването на правоъгълници. В средата на април те представят стратегия. Тя включва вграждане на лентата в специална версия на четиримерно пространство. С обикновено вграждане може да се постави вградения обект по какъвто и да е начин. Например да се вгради двумерен затворен контур в двумерна равнина. Броят на начините, по които може да се направи, е толкова неограничен, колкото и броя на начините, по които може да се постави огърлица на маса.
Но да предположим, че двумерната повърхност, в която ще се вгради контурът, има някаква структура. Например карта със стрелки (наречени вектори), показваща в коя посока и с каква скорост вятърът духа във всяка точка на Земята. Това е например двумерна повърхност с допълнителна информация или структура във всяка точка.
След това може да наложим ограничението, че едномерният затворен контур трябва да бъде вграден в тази карта, така че винаги да следва посоката на стрелките, сред които е вграден.

Диаграма, показваща как геометричните обекти могат да бъдат вградени в пространства с по-голяма размерност. Кредит: Samuel Velasco/Quanta Magazine.
Други видове геометрични пространства позволяват да се въведат други видове ограничения. Това, което се оказа важно за работата на Грийн и Лоб, се нарича симплектично пространство. Тази странна дума идва от гръцкото симплетикос(συμπλεκτικός), което означава "сплитане заедно", от syn (заедно) и plekein (плетиво)
Този тип геометрична среда се появява за първи път през 19 век с изучаването на физически системи като орбитални планети. Когато една планета се движи през тримерно пространство, нейната позиция се определя от три координати. Но ирландският математик Уилям Роуън Хамилтън забелязва, че във всяка точка на движение на планетата е възможно да се постави вектор, представящ импулса на планетата.
През 80-те години математик на име Владимир Арнолд (Vladimir Arnold) разработва математическото изследване на симплектичната геометрия. Той разбира, че геометричните пространства със симплектична структура се пресичат при въртене по-често от пространствата без такава структура.
Това подхожда идеално за Грийн и Лоб, за да разрешат проблема с вписаните правоъгълници за всички съотношения, като доказват, че въртящото се копие на параметризиращата лента на Мьобиус също се пресича много. Така те започват да се опитват да вграждат двумерната лента на Мьобиус в четиримерно симплектично пространство.
До края на април Грийн и Лоб определят, че е възможно да се вгради лентата на Мебиус в четиримерно симплектично пространство по начин, който да съответства на структурата на пространството. След това могат да започнат да използват инструментите на симплектичната геометрия - много от тях се отнасят директно към въпроса как се пресичат пространствата.
„Ако можем да накараме [лентата на Мебиус] да следва симплектични правила, можем да се възползваме от някои симплектични теореми“, заяви Лоб.
От този момент Грийн и Лоб вече са уверени, че могат да се подобрят в резултата на Хугелмайер - което означава, че могат да докажат, че повече от една трета от всички ротации произвеждат пресечна точка. Това от своя страна би означавало, че правоъгълници с повече от една трета от всички съотношения на страните могат да бъдат намерени като точки на всяка затворена крива.
Но резултатът идва много по-бързо, отколкото очакват. И причината за това е свързана с причудлив математически обект, наречен бутилката на Клайн, който има важно свойство, когато се разглежда в контекста на симплектичната геометрия.
Връзката с бутилката на Клайн
Бутилката на Клайн подобно на лентата на Мьобиус, има само една страна и всъщност можее да направите такава, като залепите две ленти на Мьобиус.
Всяка бутилка на Клайн, която бихте могли да направите и поставите на бюрото си, както правят много математици, преминава през себе си. Няма начин да вградите бутилката на Клайн в триизмерно пространство, без да се пресича.
Това не винаги е така. В четиримерно пространство е възможно да вградите бутилката на Клайн така че да не се пресича. Четвъртото измерение осигурява допълнително пространство за маневриране, което позволява на бутилката на Клайн да избегне пресичането. Подобно е на това как двама души, които вървят един към друг по едномерна линия и не могат да не се сблъскат, но двама души, приближаващи се един към друг на двуизмерен под, могат лесно да се отклонят от пътя.
 Илюстрация на бутилка Клайн. Кредит: Samuel Velasco/Quanta Magazine.
Илюстрация на бутилка Клайн. Кредит: Samuel Velasco/Quanta Magazine.
През май Грийн и Лоб се сещат за един интересен факт за бутилката на Клайн: Невъзможно е да се вгради в четиримерно симплектично пространство така, че да не се пресича. С други думи, няма такова нещо като непрекъсната бутилка на Клайн, която да съответства на специалните правила на симплектичното пространство. Този факт е ключът към доказателството.
Ето защо. Грийн и Лоб вече демонстрираха, че е възможно да се вгради лентата на Мебиус в четиримерно симплектично пространство по начин, който следва правилата на пространството. Това, което им трябва да разберат, е дали всяко завъртане на лентата на Мьобиус пресича оригиналното копие.
Двете Мьобиусови ленти се свръзват в бутилка на Клайн чрез обикновена двустранна лента, чиято задна и предна повърхност са оцветени в бяло и синьо, съответно. Анимация от Konrad Polthier.
Да, две ленти на Мьобиус, които се пресичат помежду си, са еквивалентни на бутилка на Клайн, която се пресича в този тип пространство. И ако завъртите лента на Мьобиус, така че завъртяното копие да не се пресича с оригиналното копие, по същество сте създали бутилка на Клайн, която не се пресича. Но такава бутилка на Клайн е невъзможна в четиримерно симплектично пространство. Следователно, всяко възможно завъртане на вградената лента на Мьобиус също трябва да се пресича, което означава, че всяка затворена, гладка крива трябва да съдържа набори от четири точки, които могат да бъдат съединени заедно, за да образуват правоъгълници с всякакви пропорции.
Доказателството на Грийн и Лоб е добър пример за това как решаването на проблем често зависи от намирането на подходящата гледна точка, от която да се обмисли. Поколения математици не успяха да се справят с тази версия на задачата с вписаните правоъгълници, защото се опитваха да я решат в по-традиционни геометрични среди. След като Грийн и Лоб я преместиха в симплектичния свят, задачата отстъпи лесно.
„Тези задачи, формулирани около 1910-те и 1920-те, не разполагаха с подходящата рамка“, коментира Грийн. „Това, което сега осъзнаваме, е, че те наистина са скрити въплъщения на симплектичните явления.“
Справка:
The Rectangular Peg Problem
Joshua Evan Greene, Andrew Lobb, arXiv:2005.09193
Източник:
New Geometric Perspective Cracks Old Problem About Rectangles, Quanta Magazine



















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
Прост Човек
Стъклените бутилки съдържат 5 до 50 пъти повече микропластмаси от пластмасовите бутилки
dolivo
Най-старите "човешки" фосили в Япония, се оказаха нечовешки, твърди ново проучване
dolivo
Как „зеленото побутване“ стимулира устойчивите избори на хората
helper68
Натурални суперколайдери: Черните дупки могат да се използват ускорители на частици