
Тазгодишната награда Абел е присъдена на американския математик Денис Съливан за новаторска работа в редица математически теми. Наградата Абел е едно от най-високите отличия в математиката.
Според изявление на Норвежката академия на науката и литературата (DNVA), която раздава наградата всяка година заедно с награда, равняваща се на около $864 000 ($7,5 милиона норвежки крони), Денис Съливан (Dennis Sullivan) е отличен "за своя новаторски принос към топологията в неговия най-широк смисъл, и по-специално неговите алгебрични, геометрични и динамични аспекти."
Съливан всъщност работи в невероятно разнообразие от математически области. Те включват топология, която изучава геометрични форми, без да обръща внимание на точни геометрични величини като дължини, площи или ъгли и динамични системи. Както често се случва с брилянтните математици, способността на Съливан да прави връзки между привидно различни области е ключът към неговия успех. Според изявлението на наградата „Абел“ , „настойчивото търсене на Денис Съливан за фундаментално разбиране и способността му да вижда аналози между различни области на математиката и да изгражда мостове между тях, завинаги промениха тази област“.
Подскачане по числовата ос
В областта на топологията Съливан прави важен принос за нещо основно в областта: разбирането на всички топологични форми, които съществуват в дадено измерение. Както подсказва името, динамичните системи включват някаква промяна, която може да бъде описана с математически изрази.
Като пример да вземем уравнението:
y=x2
То не изглежда особено динамично, докато не осъзнаем, че може да го прилагаме отново и отново. Например представете си, че сте на числовата права в точката x=2 и сте решили да прескочите до числото, което се получава, когато включите x=2 уравнението. Това число е
y=22=4
така че прескачате две единици наведнъж. Ако сега приложите уравнението отново към този резултат, се получава
y=42=16
и преминаваме напред към 16 Прилагането му отново към последния резултат дава
y=162=256
с което правим доста голям скок. Извършвайки това за неопределено време (това се нарича итерация) ще откриете, че вашето движение по числовата права се дава от последователността
2,4,16,256,65536,4294967296...
което се нарича орбита на началната стойност x=2
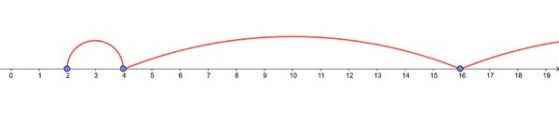 Подскачане по числовата права.
Подскачане по числовата права.
Орбитата, която се получава, може да зависи много от първоначалната стойност, която изберете. Защото x=2 вашето пътуване ви отвежда бързо към безкрайността, но за първоначалната стойност x=1/2 ви отвежда към 0 на непрекъснато намаляващи стъпки:
1/2, 1/4, 1/16, 1/256, ....
И ако започнете от x=0, щяхте да заседнете там, където сте, тъй като
02=0
Хаос и фрактали
Динамиката в примера по-горе е ограничена до числовата права, но има начин (използвайки комплексни числа) да направим уравнения като горното да насочват движението на точките в двумерната равнина. Можем да започнем в която и да е точка от равнината и уравнението щв ни кажв къде да скочим по-нататък, като итерацията ще ни отведе на безкрайно пътуване по равнината.
Динамиката, която възниква, е изследвана в началото на двадесети век за семейство уравнения, известни като рационални карти - примерът по-горе е член на това семейство. Но едва когато компютрите позволиха да се изчисляват дълги части от орбитата на първоначалната стойност и да се начертаят тези орбити, са разкрити умопомрачително красиви картини като следните.

Множеството на Жулиа, свързано с функцията y = x 2 -1. Множествoтo Жулиа е обозначено в бяло. Останалата част от изображението (зелените и сините зони) принадлежат на множеството на Фату. Както можете да видите, множеството на Фату се състои от много отделни компоненти в този случай.
(Вижте прозорецът вдясно, за да разберете какво представляват рационалните карти – строго погледнато, те са дефинирани върху сферата на Риман, а не върху равнината.)
Картината по-горе показва множеството на Жулиа, свързан с уравнението y=x2-1 (когато се прилага към комплексни числа). Множествата Жулиа са кръстени на математика Гастон Жулиа (Gaston Julia) и представляват един вид вододел на динамиката, основана на уравнения: точките от множеството на Жулиа се държат много различно от тези около тях. Орбитите, които започват от множеството на Жулиа, винаги остават на множеството на Жулиа и динамиката там е хаотична в математически смисъл: дори две начални стойности да са невероятно близки една до друга, техните орбити не остават толкова близо една до друга. Множествата на Жулиа от рационални карти обикновено са фрактали със спираща дъха сложност.
Останалата част от равнината, състояща се от всички точки, които не са в множеството на Жулиа, се нарича множеството на Фату, на името на математика Пиер Фату (Pierre Fatou). Орбитите, които започват в множеството на Фату, винаги остават на множеството на Фату, но този път динамиката е по-подредена. Най-общо казано, орбитите, които започват близо една до друга, остават близо една до друга. Технически погледнато, динамиката е равнопостоянна на множеството на Фату. (Повече по темата в Нов мост между фракталната геометрия и динамиката на частичната синхронизация)

Друго множество на Жулиа, показано в зелено, този път за функцията y = x 2 + c, където c е приблизително равно на комплексното число -0,51+ i 0,52. Синята зона принадлежи на множеството на Фату. В този случай множеството на Фату се състои само от един компонент. Кредит: Morn, CC BY-SA 4.0.
Без блуждаещи компоненти
След откриването на красивите структури, свързани с рационалните карти, се появяват множество въпроси. Както можете да се види в графиките по-горе, множеството на Фату се състои от компоненти, които са разделени един от друг с части от множеството на Жулиа. И въпреки че може да не успеете да го видите, защото компонентите са твърде малки, може да има безкрайно много от тях. Такъв е случаят с картинката по-горе. На втората илюстрация множеството на Фату се състои само от един компонент, показан в синьо.
Ако приложите съответното уравнение към цял компонент, ще откриете, че то е преместено акуратно върху друг компонент (който може да бъде същият). Един въпрос, който възникна естествено, когато хората за първи път са изучавали динамиката на рационалните карти, бе дали може да има компонент, чиято орбита посещава безкрайно много други компоненти, без изобщо да става периодична. Такъв компонент ще се нарече блуждаещ домейн.
Това бе лесен за задаване въпрос, на който се оказа, че отговорът е невероятно труден. Но през 1985 г., когато въпросът е вече над 60-годишен, Съливан намира решение, което получава огромно признание. Неговата теорема за домейни показва, че орбитите на всички компоненти от множеството на Фату на рационална карта в крайна сметка стават периодични, движейки се през един и същ цикъл от компоненти отново и отново.
Осъществяването на връзката
За да докаже теоремата за липса на блуждаещи домейни, Съливан прави брилянтна връзка с резултат от клас динамични системи, които на пръв поглед изглеждат много различни от тези, които се получават от рационалните карти. Трансформацията на Мьобиус е израз на формулата:
където a, b, c и d могат да бъдат реални или комплексни числа. Два примера са
Трансформацията на Мьобиус сама по себе си е пример за рационална карта, но за разлика от други рационални карти, колекциите от трансформации на Мьобиус могат да образуват самостоятелни структури, наречени групи (За да разберете какво представляват групите: "Теорията на групите - една усмивка само"). Както и преди с рационалните карти, използването на комплексни числа дава възможност за прилагане на трансформацията на Мьобиус към точка в равнината, като в резултат се получава друга точка в равнината. По този начин, когато имате група трансформации на Мьобиус и някаква начална точка, може да разгледате всички точки, където тези трансформации приемат началната точка, като отново се получава един вид орбита.
Удивително е, че динамиката на такава група трансформации на Мьобиус може да генерира фрактали, много подобни на тези, произтичащи от рационалните карти, разделяйки равнината на аналог на множеството на Фату и аналог на множеството на Жулиа (вижте тази статия, за да научите повече).

Това изображение изобразява граничното множество от група трансформации на Мьобиус. Много прилича на множеството на Жулиа. Това изображение е създадено от Дейвид Райт и за първи път се появява в Plus Magazine.
Никой математик не може да устои на такъв примамлив паралел и Съливан не е изключение. През 1980-те той публикува речник, който превежда понятия в динамиката на рационалните карти в понятия в динамиката на групи на Клайн (за Клайн "Бутилката на Клайн - играчка за математици"), които са определени групи от трансформациите на Мьобиус. Работата се оказа основополагаща в областта, позволявайки на хората да докажат резултати в едната част от речника, използвайки инструменти, разработени за другата.
По-общо казано, работата на Съливан върху динамичните системи намери универсални характеристики и основни принципи в конформната динамика, подполе на теорията на динамичните системи, което включва вида уравнения, които се разглеждат в тази статия.
Можем да се каже още много за работата на този „харизматичен и жизнен член на математическата общност“, както го описва Алекс Белос в кратката си биография. „[Съливан] се прескача от област в област, привидно без усилие, използвайки алгебрични, аналитични и геометрични идеи като истински виртуоз“, се казва в изявлението от наградата Абел, която описва и други аспекти от работата на Съливан.
Източник:
The Abel Prize 2022: Dennis Sullivan
Marianne Freiberger, Plus Magazine























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?
Nikor
На 30 септември 1928 е открит пеницилинът
Прост Човек
Ново обяснение за гигантските експлодиращи кратери в Сибир